解答题(本大题共小题， 共分)
-
1.(本小题10分)
如图1所示，在△ABC中，点O是AC上一点，过点O的直线与AB，BC的延长线分别相交于点M，N．
-
2.(本小题10分)
如图1，正方形ABCD和正方形QMNP，M是正方形ABCD的对称中心，MN交AB于F，QM交AD
于E．
（1）猜想：ME与MF的数量关系；
（2）如图2，若将原题中的“正方形”改为“菱形”，且∠QMN=∠ABC，其他条件不变，探索线段ME与线段MF的数量关系，并加以证明；
（3）如图3，若将原题中的“正方形”改为“矩形”，且AB:BC=1:2，其他条件不变，探索线段ME与线段MF的数量关系，并说明理由；
（4）如图4，若将原题中的“正方形”改为“平行四边形”，且∠QMN=∠ABC，AB:BC=m，其他条件不变，求出ME:MF的值．（直接写出答案）
-
3.(本小题10分)
我们定义：如图1，在△ABC中，把AB绕点A顺时针旋转α（0°<α<180°）得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′．
当α+β=180°时，我们称△AB′C′是△ABC的“旋补三角形”，△AB′C′边B′C′上的中线AD叫做
△ABC的“旋补中线”，点A叫做“旋补中心”．
特例感知：
（1）在图2、图3中，△AB′C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．
①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD= BC；
②如图3，当∠BAC=90°，BC=8时，则AD的长为 ．
猜想论证：
（2）在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．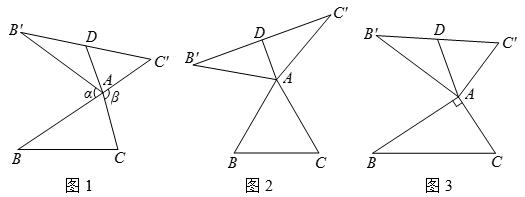
拓展应用
（3）如图4，四边形ABCD，∠C=90°，∠D=150°，BC=12，CD=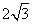
，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，请给予证明，并求△PAB的“旋补中线”长；若不存在，请说明理由．
，DA=6．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，请给予证明，并求△PAB的“旋补中线”长；若不存在，请说明理由．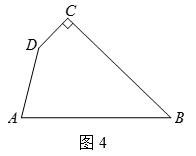
-
4.(本小题10分)
如图1，已知正方形ABCD在直线MN的上方，BC在直线MN上，E是射线BC上一点，以AE为边在直线MN的上方作正方形AEFG．
（1）连接FC，观察并猜测tan∠FCN的值，并说明理由；
（2）如图2，将图1中正方形ABCD改为矩形ABCD，AB=m，BC=n（m，n为常数），E是射线BC上一动点（不含端点B），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上，当点E沿射线CN运动时，请用含m，n的代数式表示tan∠FCN的值．
