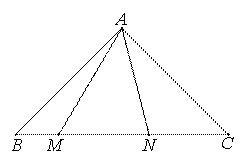
如图，等腰直角三角形ABC中，AB=AC，∠A=90°，M，N为斜边BC上两点且∠MAN=45°，则BM、CN、MN之间的数量关系是（）

要找BM、CN、MN三者之间的数量关系，考虑到根据题目条件中出现了“大角夹半角”模型，所以考虑用旋转．旋转需要考虑相等的边，在这里可以利用等腰三角形两边相等，那么不妨把△ABM旋转出去，如图所示，接下来注意到旋转之后△ABM≌△ACD，那么可以得到AD=AM，BM=DC，∠CAD=∠BAM，∠ABM=∠ACD=45°，可得∠NCD=90°，并且∠DAN=∠CAD+∠CAN=∠BAM+∠CAN=45°=∠MAN，那么可以得到△MAN≌△DAN，进而MN=DN；那么在直角三角形DCN中，ND²=NC²+DC²，所以BM²+CN²=MN²．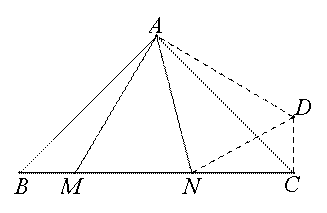

略