如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在A′的位置上．若OB=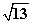
，
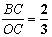，求点A′的坐标.
答案
如图，过点A′作A′D⊥x轴，交x轴于点D；
过点B作BE⊥y轴，交DA′的延长线于点E.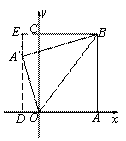
在矩形OABC中，
由OB=
，
知，OA′=BC=2，A′B=OC=3，
由题意知，∠A′=90°，
∴△A′OD∽△BA′E，且相似比为2:3，
设OD=2x，
则A′E=3x，BE=2+2x，A′D=
∴DE=+3x=OC=3，
∴x=
∴点A′的坐标为（
）.
知识点：相似三角形的判定与性质
分析基本图形，在矩形OABC中，由OB=,，可得矩形的长与宽分别为3和2；而且由折叠可得∠A′=∠A=90°，要求点A′的坐标，我们可以想到构造双垂直模型来解决。
略
WORD格式（
