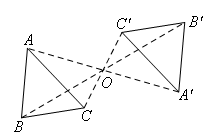
如图,△ABC与△A′B′C′成中心对称,则下列结论不正确的是( )
- A.S△ABC=S△A′B′C′
- B.AB=A′B′,AC=A′C′,BC=B′C′
- C.∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,∠BAC=∠B′A′C′
- D.S△ACO=S△A′B′O
答案
正确答案:D
知识点:略
解题要点:
中心对称的定义:把一个图形绕着某一点旋转180°,如果它能够与另一个图形
重合,那么就说这两个图形关于这个点对称或中心对称.
中心对称的性质:中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
解题过程:
A.中心对称的两个图形形状相同、大小相等,S△ABC=S△A′B′C′,故A正确;
B.由中心对称的定义及性质可得AB=A′B′,AC=A′C′,BC=B′C′,故B正确;
C.由中心对称的定义及性质可得∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,∠BAC=∠B′A′C′,故C正确;
D.S△A′B′O=S△ABO≠S△ACO,故D错误.
略








