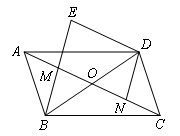
（2020鄂州）如图，在平行四边形ABCD中，对角线AC与BD交于点O，点M，N分别为OA，OC的中点，延长BM至点E，使EM=BM，连接DE．
（1）求证：△AMB≌△CND；
（2）若BD=2AB，且AB=5，DN=4，求四边形DEMN的面积．

解：（1）∵平行四边形ABCD中，对角线AC与BD交于点O，
∴AO=CO，
又∵点M，N分别为OA，OC的中点，
∴AM=CN，
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∴∠BAM=∠DCN，
∴△AMB≌△CND（SAS）；
（2）∵△AMB≌△CND，
∴BM=DN，∠ABM=∠CDN，
又∵BM=EM，
∴DN=EM，
∵AB∥CD，
∴∠ABO=∠CDO，
∴∠MBO=∠NDO，
∴ME∥DN
∴四边形DEMN是平行四边形，
∵BD=2AB，BD=2BO，
∴AB=OB，
又∵M是AO的中点，
∴BM⊥AO，
∴∠EMN=90°，
∴四边形DEMN是矩形，
∵AB=5，DN=BM=4，
∴AM=3=MO，
∴MN=6，
∴矩形DEMN的面积=6×4=24．

略