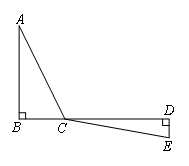
如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC．已知AB=5，DE=1，BD=8，设CD=x．
（1）用含x的代数式表示AC+CE的长；
（2）求AC+CE的最小值；
（3）根据（2）中的规律和结论，请构图求出代数式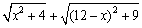的最小值．

解：（1）设CD=x，则BC=8-x，
在Rt△ABC中，AC，
在Rt△CDE中，CE，
所有AC+CE=，
（2）当A、C、E共线时，AC+CE的值最小，即AC+CE的最小值为AE的长，
即C点为AE与BD的交点，
作EF⊥AB于F，如图1，

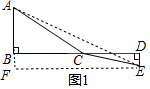
则BF=DE=1，EF=BD=8，
在Rt△AEF中，AE
即AC+CE的最小值为10，
故答案为10；
（3）如图2，AB=3，DE=2，BD=12，

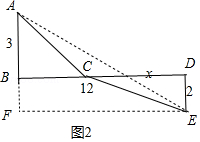
代数式的最小值为AE的长，即它的最小值为13．
故答案为13．

略