如图，在△ABC中，AB=AC=2，∠B=∠C=40°，点D在线段BC上运动（点D不与点B，C重合），连接AD，作∠ADE=40°，DE交线段AC于点E．
（1）当∠BDA=115°时，∠BAD= °，∠EDC= °，∠DEC= °；在点D从B向C运动的过程中，∠BDA逐渐变 （填“大”或“小”）；
（2）当DC等于多少时，△ABD≌△DCE，请说明理由．
答案
（1）25，25，115，小；
（2）当DC等于2时，△ABD≌△DCE，理由略．
知识点：全等三角形的判定和性质
（1）∵在△BAD中，∠B=∠C=∠40°，∠BDA=115°，
∴∠BAD=180°-∠B-∠BDA=180°-40°-115°=25°；
∠EDC=180°-∠ADB-∠ADE=180°-115°-40°=25°．
∠DEC=180°-∠C-∠EDC=180°-40°-25°=115°
∵∠BDA=∠C+∠CAD=40°+∠CAD
因为点D从B向C运动的过程中，∠CAD逐渐变小，
所以∠BDA逐渐变小
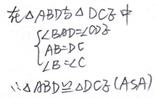
略
WORD格式（
