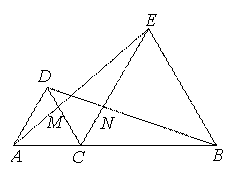
如图，点C为线段AB上一点，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论： ①△ACE≌△DCB； ②CM＝CN；③AC=DN其中，正确结论的个数是()个．

∵△DAC和△EBC都是等边三角形
∴AC=CD，CE=BC，∠ACD=∠ECB=60°
∴∠ACE=∠DCB
∴△ACE≌△DCB（SAS）（①正确）
∴∠AEC=∠DBC
∵∠DCE+∠ACD+∠ECB=180°，∠ACD=∠ECB=60°
∴∠DCE=∠ECB=60°
∵CE=BC，∠DCE=∠ECB=60°，∠AEC=∠DBC
∴△EMC≌△BNC（ASA）
∴CM=CN（②正确）
∵AC=DC
在△DNC中，DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC＞60°，而DN所对的角为60°，
根据三角形中等边对等角、大边对大角，小边对小角的规律，
则DC＞DN，即是AC＞DN，所以③错误，所以正确的结论有两个．故选C．

略