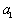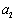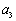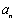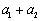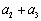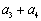古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记作，第二个三角数记作，第三个三角数记作…，第n个三角数记作，计算，，，…，由此推算(    )

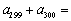• A.
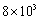
• B.
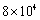
• C.
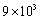
• D.

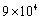
答案

正确答案：D

知识点：有理数的乘方  科学记数法  规律探究  

因为a¹＋a²＝1＋3＝4＝2²；
a²＋a³＝3＋6＝9＝3²；
a³＋a⁴＝6＋10＝16＝4²；
所以aⁿ＋a^n＋1＝（n＋1）²；
所以a²⁹⁹＋a³⁰⁰＝300²=90000=．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>