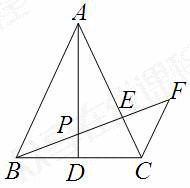
已知：如图，△ABC中，AB＝AC，AD是中线，P是AD上一点，过C作CF∥AB，延长BP交AC于E，交CF于F．
求证：BP²＝PE·PF．

答案

证明: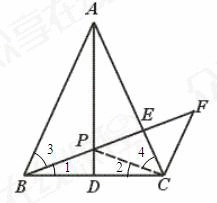
∵AB＝AC，AD是中线，
∴AD⊥BC,BP=CP
∴∠1=∠2
又∵∠ABC=∠ACB
∴∠3=∠4
∵CF∥AB
∴∠3=∠F,∠4=∠F
又∵∠EPC=∠CPF
∴△EPC∽△CPF
∴
∴CP^2＝ BP²＝PE·PF
即证所求

知识点：相似之共线线段的比例问题  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>