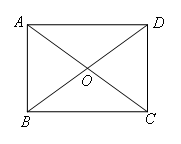
如图，四边形ABCD中，对角线AC，BD相交于点O，AO=OC，BO=OD，且∠AOB=2∠OAD．若∠AOB:∠ODC=4:3，则∠ADO的度数为(    )

∵AO=OC，BO=OD
∴四边形ABCD是平行四边形
∵∠AOB=2∠OAD，∠AOB=∠OAD+∠ADO
∴∠OAD=∠ADO
∴AO=OD
∴OC=OD，AC=BD
∴平行四边形ABCD是矩形，∠ODC=∠OCD
∴∠ADC=90°
∵∠AOB:∠ODC=4:3
∴∠COD:∠ODC:∠OCD=4:3:3
∵∠COD+∠ODC+∠OCD=180°
∴∠ODC=54°
∴∠ADO=36°

略