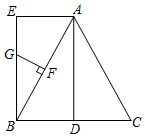
如图，在△ABC中，AB=AC，D是BC中点，过点A作AE∥BC，使AE=BD，取AB中点F，作GF⊥AB，交EB于点G，若AD=8，BD=4，则四边形ADBE为      ，EG的长为      .(    )

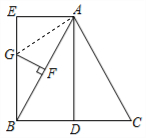
∵AE∥BC，AE=BD
∴四边形AEBD是平行四边形
∵AB=AC，D是BC中点
∴AD⊥BC
∴∠ADB=90°
∴四边形AEBD是矩形
连接AG
∵F是AB的中点，GF⊥AB
∴GA=GB
∵四边形AEBD是矩形，AD=8，BD=4
∴EB=AD=8，EA=BD=4，∠E=90°
设EG=x，则GB=GA=8-x
在Rt△AEG中
∵EA²+EG²=AG²
∴4²+x²=(8-x)²
∴x=3，
即EG=3

略