勾股定理最早出现在商高的《周髀算经》：“勾广三，股修四，经隅五”．观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1．柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为2m（m≥3，m为正整数），则其弦是(    )

• A.
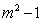
• B.
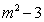
• C.
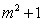
• D.

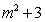
答案

正确答案：C

知识点：直角三角形的判别条件  

因为2m为偶数，
所以设其股为a，则弦为a+2，
由勾股定理得：，
解得：a=，
所以a+2=，
故选：C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>