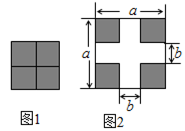
如图，将大小相同的四个小正方形按照图1和图2所示的两种方式放置于两个正方形中，根据两个图形中阴影部分的面积关系，可以验证的公式是（ ）
- A.(a-b)2=a2-2ab+b2
- B.(a+b)2=a2+2ab+b2
- C.(a-b)2=(a+b)2-4ab
- D.(a+b)(a-b)=a2-b2
答案
正确答案：A
知识点：略
阴影部分的面积是四个阴影小正方形的面积和，由拼图可得四个阴影小正方形可以拼成边长为(a-b)的正方形，因此①的面积为(a-b)2，
由②可知，阴影部分的面积等于边长为a的正方形的面积减去之间十字架的面积，即：a2-2ab+b2，
因此有(a-b)2=a2-2ab+b2．
故选A
略
WORD格式（
