正方形ABCD中，E为BC上的一点，F为CD上的一点，BE+DF=EF，则∠EAF的度数为( )
- A.30°
- B.37.5°
- C.45°
- D.60°
答案
正确答案：C
知识点：三角形全等的判定及性质
延长EB至点G，使得BG=DF，连接AG，可证明：△ABG≌△ADF（SAS），∴∠DAF=∠BAG，AF=AG，又∵EF=DF+BE=EB+BG=EG，AE=AE∴△AEG≌△AEF（SSS）∴∠EAG=∠EAF，∵∠DAF+∠EAF+∠BAE=90°∴∠EAG+∠EAF=90°，∴∠EAF=45°。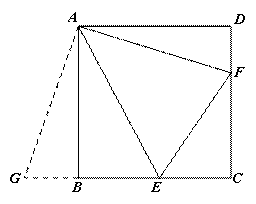
略
WORD格式（
