如图，在△ABC中，ABC＝90°，AB=6m，BC=8m，动点P以2m/s的速度从A点出发，沿AC向点C移动．同时，动点Q以1m/s的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动．设移动的时间为t秒．
（1）①当t=2.5s时，求△CPQ的面积；
②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；
（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，求出t的值．

答案

解：（1）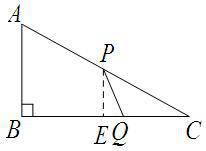
过点P作PE⊥BC交BC于E
∵AB=6m，BC=8m
∴AC＝10m
∵∠B=90°，PE⊥BC
∴PE∥AB
①当t＝2.5s时，PC＝10﹣2t＝5m，QC＝t＝2.5m
∵PC＝5m＝
∴PE是△ABC的中位线
∴PE＝＝3m
∴S_△CPQ＝＝×2.5×3＝（m²）
②∵P点从A到达C需要5s，Q点从C到达B需要8s，由题意：当其中有一点到达终点时，它们都停止移动．
∴t的范围：0≤t≤5
又∵△PEC∽△ABC
∴，即
∴PE＝
∴S＝＝×＝

知识点：相似中的动点问题  

略

略

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>