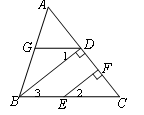
如图，已知BD⊥AC，EF⊥AC，D、F为垂足，G是AB上一点，且∠l=∠2．判断∠AGD和∠ABC的数量关系？并说明你的理由．

答案

∠AGD=∠ABC，理由如下：
∵BD⊥AC，EF⊥AC（已知）
∴BD∥EF（同位角相等，两直线平行）
∴∠2=∠3（两直线平行，同位角相等）
∵∠1=∠2（已知）
∴∠1=∠3（等量代换）
∴DG∥BC（内错角相等，两直线平行）
∴∠AGD=∠ABC（两直线平行，同位角相等）

知识点：平行线的判定  平行线的性质  

解：∠AGD=∠ABC，理由如下：
∵BD⊥AC，EF⊥AC（已知）
∴BD∥EF（同位角相等，两直线平行）
∴∠2=∠3（两直线平行，同位角相等）
∵∠1=∠2（已知）
∴∠1=∠3（等量代换）
∴DG∥BC（内错角相等，两直线平行）
∴∠AGD=∠ABC（两直线平行，同位角相等）

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>