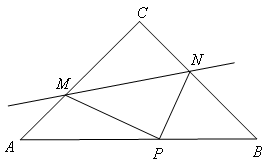
在△ABC中，AC=BC，∠ACB=90°，点M是AC上的一点，点N是BC上的一点，沿着直线MN折叠，使得点C恰好落在边AB上的P点，求证：MC：NC=AP：PB．
答案
过点M作ME⊥AB于M，过点N作NF⊥AB于F
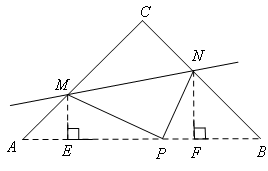
△MAE是等腰直角三角形，ME=AE
△NFB是等腰直角三角形，NF=BF
∵∠MEP=∠MPN=∠PFN=90°（双垂直模型）
∴△MEP∽△NFP，
∴MP：PN=ME：PF=EP：NF，即MP：PN=AE：PF=EP：BF
利用等比性质得
AE+EP：PF+BF=AP：PB=MP：PN
即MC：NC=AP：PB．
知识点：相似三角形的判定与性质
略
不能熟练应用等角的外角相等这一性质
WORD格式（
