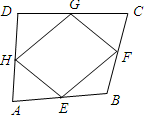
(2011湖南改编)如图所示,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接EF、FG、GH、HE.
(1)请判断四边形EFGH的形状,并给予证明;
(2)四边形EFGH可能是菱形,请给出判断依据;
(3)四边形EFGH可能是矩形,请给出判断依据;
(4)四边形EFGH可能是正方形,请给出判断依据;
答案
(1)四边形EFGH的形状是平行四边形.
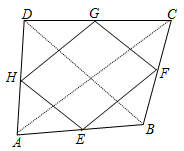
证明:连接AC、BD,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF∥AC,EF= AC,HG∥AC,HG=
AC,GF=
BD,
∴EF=HG,EF∥HG,
∴四边形EFGH是平行四边形.
(2)添加的条件是AC=BD.
∵EF= AC ,GF=
BD , AC=BD
∴EF =GF
又∵四边形EFGH是平行四边形.
∴四边形EFGH是菱形
(3)添加的条件是AC⊥BD.
∵四边形EFGH是平行四边形.AC⊥BD
∴EF ⊥GF
又∵四边形EFGH是平行四边形.
∴四边形EFGH是矩形
(4)添加的条件是AC⊥BD且AC=BD
由(2)(3)我们可以知道四边形EFGH是正方形
知识点:三角形中位线定理 平行四边形的判定与性质 菱形的判定与性质 矩形的判定与性质 正方形的判定与性质
(1)连接AC、BD,根据三角形的中位线定理得到EF∥AC,EF= AC,HG∥AC,HG=
AC,推出EF=HG,EF∥HG即可;
(2)根据三角形的中位线定理得到EF= AC,GF=
BD,AC=BD,推出EF=GF,由(1)即可推出答案.
(3)根据三角形的中位线定理得到EF= AC,GF=
BD,AC⊥BD,推出EF⊥GF,由(1)即可推出答案.
(4)根据(2)和(3)我们可以知道AC=BD且AC⊥BD时,四边形EFGH可能正方形
本题主要考查对三角形的中位线定理,平行四边形,菱形,矩形,正方形的判定等知识点的理解和掌握,能求出四边形是平行四边形是证此题的关键.一部分同学在这部分掌握不牢固。








