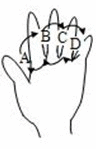
右图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4…,当数到14时,对应的字母是 _______;当字母C第2011次出现时,恰好数到的数是________;当字母C第2n+1次出现时(n为正整数),恰好数到的数是__________(用含n的代数式表示).
答案
B; 6033;6n+3
知识点:规律探索型问题
由题意知,A→B→C→D→C→B为一个循环,可知14数字对应的应该是B,观察可得每一个循环中C出现两次,而C第2011次出现的时候可知循环了1005次,并且又数了三个数到C,6×1005=6030,6030+3=6033,可知恰好数到的数为6033.而当C第2n+1次出现的时候,可知循环了n次,并往前数3个数,可知这个数为6n+3.
1、不能正确的找到循环节 2、不能找到每一次循环C出现两次,从而找到循环的次数和数的数之间的关系








