如图，在梯形ABCD中，AD∥BC，E是BC的中点，AD=5，BC=12，CD=，∠C=45°，点P是BC边上一动点，设PB的长为x．

（1）当x的值为            时，以点P、A、D、E为顶点的四边形为直角梯形；
（2）当x的值为            时，以点P、A、D、E为顶点的四边形为平行四边形；（3）点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？试说明理由．

答案

（1）3或8；（2）1或11；（3）当x的值为11时，以P、A、D、E为顶点的四边形构成菱形解：
（1）①当P运动到如图位置时

即PA⊥BC时，四边形APED为直角梯形，此时过点D作DF⊥BC交BC于点F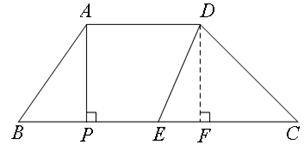

则PF=AD=5
由CD=，∠C=45°
得：DF=FC=4
∴x=PB=12-4-5=3
②当P点运动到如图位置时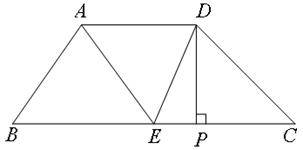

即PD⊥BC时，此时四边形AEPD为直角梯形
此时由PC=4
得：x=BP=12-4=8
（2）①当P运动到如图时，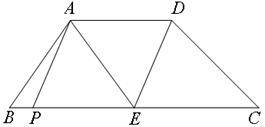

即AP∥DE，此时四边形APED为平行四边形
PE=AD=5
∵E为BC的中点
∴BE=6
∴x=PB=6-5=1
②当P运动到如图时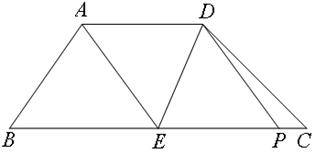

此时AE∥DP，四边形AEPD为平行四边形
∴EP=AD=5
∴x=BP=BE+EP=6+5=11
（3）要想使以P、A、D、E为顶点的四边形构成菱形,首先必须是平行四边形，故只需验证BP=1和11时，此时的平行四边形是否是菱形
当BP=1时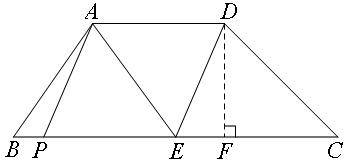

过点D作DF⊥BC于点F
∵CF=4，CE=6
∴EF=2
∴DE===
AD≠DE
∴四边形APED不是菱形
当BP=11时

过点D作DF⊥BC于点F
由DF=CF=4
得：EF=2,
∵EP=5
∴FP=3
从而DP===5
由AD=DP=5 得：四边形AEPD为菱形

知识点：四边形动点问题  

略

略

下载次数：8

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>