（2012河南）如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上一动点（不与点A、B重合），过点P做x轴的垂线交直线AB于点C，作PD⊥AB于点D．（1）求a，b及的值；（2）设点P的横坐标为m．①用含m的代数式表示线段PD的长，并求出线段PD长的最大值；②连接PB，线段PC把△PDB分成两个三角形，是否存在合适的m的值，使这两个三角形的面积之比为9:10？若存在，直接写出m的值；若不存在，说明理由．

答案

解：（1）由，得x=-2，
∴A(-2,0).由，得x=4,
∴B（4,3）.
∵，经过A、B两点，
∴
∴设直线AB与y轴交于点E，则E（0,1）.
∵PC∥y轴，
∴
∴
(2)①由（1）知，抛物线的解析式为，则点P（m,）.
已知直线AB为,则点C(m,).
∴
RtΔPCD中，
∴PD长的最大值为
②如图，分别过点D、B作DF⊥PC,BG⊥PC,垂足分别为F、G.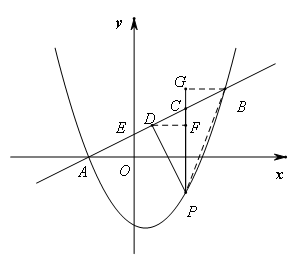

在中，.
又∵BG=4-m,
∴
 
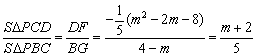
当时，解得
当时，解得

知识点：二次函数综合题  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>