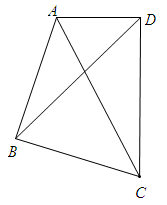
如图，四边形ABCD中，∠ABC=∠ADC=90°，且AD=2，DC=4，AB=BC，求BD的长．

答案

延长DA到E，使AE=DC，连接BD

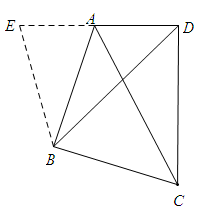
∵∠ABC=∠ADC=90°
∴∠BAD＋∠BCD=180°
又∵∠BAD+∠BAE=90°
∴∠BAE=∠BCD
∵AB=CB，AD=CD
∴△AEB≌△CDB
∴∠ABE=∠CBD，BE=BD，AE=CD=4
∴∠ABE+∠ABD=∠CBD+∠ABD=90°
∴△BDE为等腰直角三角形
∴BD===

知识点：全等三角形的判定  几何变换的类型  

略

不能熟练地对题目中图形进行旋转变换

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>