如图，延长△ABC各边，使得BF=AC，AE=CD=AB，顺次连接D、E、F，得到△DEF为等边三角形.
求证：（1）△AEF≌△CDE；
（2）△ABC为等边三角形.

答案

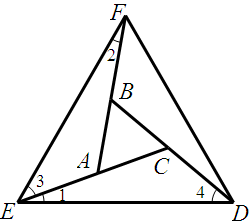
证明：（1）∵BF =AC ,AE =AB ，∴EC=FA
又△DEF为等边三角形，∴FE=ED
在△FEA和△EDC中
FE=ED
FA=EC
EA=DC
∴△FEA≌EDC
∴∠1=∠2，∠3=∠4
∴∠2+∠3=∠1+∠3=60°
∴∠1+∠4=60°
（2）∵∠BAC=∠2+∠3=60°
∠BCA=∠1+∠4=60°
∴△ABC为全等三角形。

知识点：等边三角形的判定与性质  

由全等转换角度关系，再由角度关系推出等边关系。

三角形外角性质的应用

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>