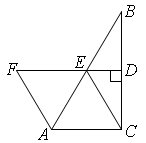如图，在△ABC中，∠ACB=90°，点E为AB中点，连结CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF=CE．求证：四边形ACEF是平行四边形．
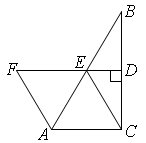
答案
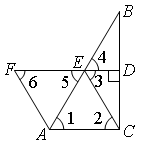
证明：∵EF⊥BC，∠ACB=90°
∴EF∥AC
∵E为Rt△ABC斜边中点
∴EC=EA
又∵AF=CE
∴∠1=∠2=∠3=∠4=∠5=∠6
从而△AEF和△EAC均为等腰三角形且底角相等
∴两顶角∠FAE=∠AEC
∴AF∥EC
∴四边形ACEF是平行四边形（一组对边平行且相等的四边形为平行四边形）
知识点：平行四边形的判定
已经知道了一组对边相等，再知道一组边上的关系即可
找AF∥EC
WORD格式（
