在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(2)若点E是线段AC上的任意一点,其它条件不变.如图2,判断线段BE、EF有怎样的数量关系并证明.小宇同学展示出如下正确的作法: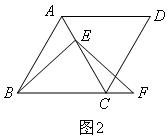
解:BE=EF,证明如下:如图2,        ①        ,

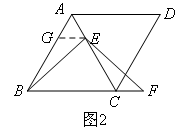
∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=120°,
∴        ②         ,
∴BE=EF;
①,②处横线上所填内容分别是()

• A.过点E作EG∥BC,交AB于点G;△BAE≌△ECF
• B.过点E作EG∥BC,交AB于点G;△BGE≌△EFC
• C.过点E作EG∥BC,交AB于点G;△BGE≌△ECF
• D.过点E作EG∥BC,交AB于点G;△BEA≌△ECF

答案

正确答案：C

知识点：类比探究问题  

略

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>