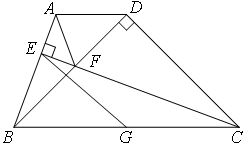
（2011重庆）如图，梯形ABCD中，AD∥BC，∠DCB=45°，CD=2，BD⊥CD．过点C作CE⊥AB于E，交对角线BD于F，点G为BC中点，连结EG、AF．
（1）求EG的长；
（2）求证：CF=AB+AF．

答案

解：（1）∵∠DCB=45°，BD⊥CD
∴△BCD为等腰直角三角形
∵CD=2
∴BC= $\sqrt{2}CD$ = $2\sqrt{2}$
EG为Rt△BCE斜边中线
∴EG= $\frac{1}{2}$ BC= $\sqrt{2}$
（2）延长BA交CD的延长线于点H

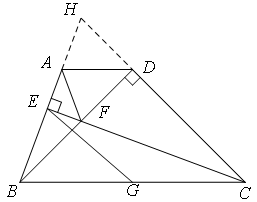
在△CDF和△BDH中
$\begin{cases} \angle DCF=\angle DBH\\ \angle BDC=\angle BDH\\ CD=BD \end{cases}$
∴△CDF≌△BDH（ASA）
∴CF=BH，DF=DH
在△AFD和△AHD中
$\begin{cases} DH=DF \\ \angle ADH=\angle ADF\\ AD=AD \end{cases}$
∴△AFD≌△AHD（SAS）
∴AF=AH
∴CF=BH=BA+AH=AB+AF