如图，已知△ABC为等边三角形，P为BC上一点，△APQ为等边三角形．（1）求证：AB∥CQ；（2）AQ与CQ能否互相垂直？若能互相垂直，指出点P在BC上的位置，并给予证明；若AQ与CQ不能互相垂直，请说明理由．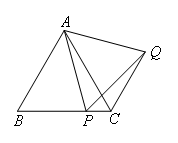
答案
（1）可证得：△ABP≌△ACQ，可得：∠ACQ=∠B=60°，从而∠ACQ=∠BAC=60°，从而AB∥CQ
（2）P为BC的中点时，AQ能垂直于CQ，由（1）得：∠ACQ=60°要满足AQ⊥CQ，那么∠CAQ=30°，此时∠CAP=30°，由三线合一得，P为BC的中点
知识点：全等三角形
略
略
WORD格式（
