如图，已知AD为△ABC的角平分线，
A，在AC上截取CE=AB，M，N分别为BC，AE的中点，求证：MN∥AD．
A，在AC上截取CE=AB，M，N分别为BC，AE的中点，求证：MN∥AD．
答案
证明：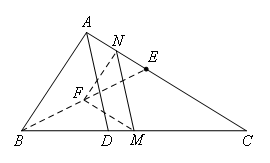
连接BE，取BE的中点F，连接FM，FN
∵M，N分别为BC，AE的中点
∴FM，FN分别为△BCE，△ABE的中位线
∴FM＝
CE，FM∥EC
FN＝AB，FN∥AB
∴∠BAC＝∠FNC，∠FMN＝∠CNM
∵CE=AB
∴FM＝FN
∴∠FMN＝∠FNM
∴∠FNM＝∠CNM
∴∠FNC＝2∠CNM
∵AD为△ABC的角平分线
∴∠BAC＝2∠CAD
∴2∠CNM＝2∠CAD，即：∠CNM＝∠CAD
∴MN∥AD
知识点：中点问题
略
略
WORD格式（
