如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．
（1）设△DPQ的面积为S，求S与t之间的函数关系式；
（2）当t为何值时，以点P，C，D，Q为顶点的四边形是平行四边形？
（3）当t为何值时，PD=PQ．
答案
解：（1）由题意知，
，AQ=t，BP=2t
∵DQ=16-t，AB=12
∴S=
(16-t)
12=-6t+96（）
（2）
时，P在线段BC上
当QD=PC时，即16-t=21-2t
∴t=5，此时四边形QPCD为平行四边形；
时，P在BC延长线上
当QD=CP时，即16-t=2t-21
∴t=
时，四边形QCPD为平行四边形．
即t=5或时，以点P，C，D，Q为顶点的四边形是平行四边形
（3）
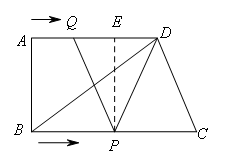
如图，过点P作PE⊥AD于点E，则四边形ABPE为矩形．
∵PE⊥AD，PQ=PD
∴QE=ED=QD
∵QD=16-t
∴QE=8-
∵AQ+QE=AE=BP
∴8-+t=2t
即t=
∴t=时，PQ=PD
知识点：四边形中的动点、存在性问题
略
略
WORD格式（
