如图,D为△ABC中线AM的中点,过M作AB、AC边的垂线,垂足分别为P、Q。过P、Q分别做DP、DQ的垂线交于点N。
(1)求证:PN=QN
(2)求证:MN⊥BC

答案
(1)连接DN
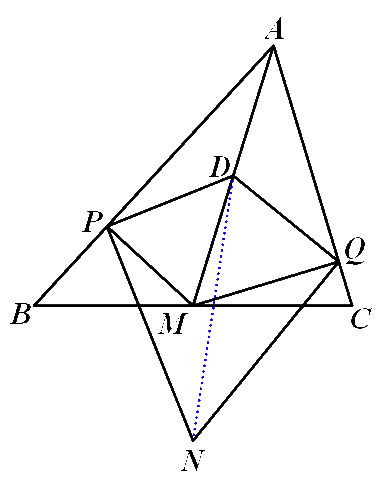
在Rt△APM中,PD为斜边上的中线
∴PD=AD=DM=AM
同理在Rt△AQM中,QD=AD=DM=AM
∴PD=QD
在Rt△PDN和Rt△QDN中
DN=DN
PD=QD
∴Rt△PDN≌Rt△QDN(HL)
∴PN=QN
(2)分别取BM、CM的中点S和T,连接PS、SN、QT和TN
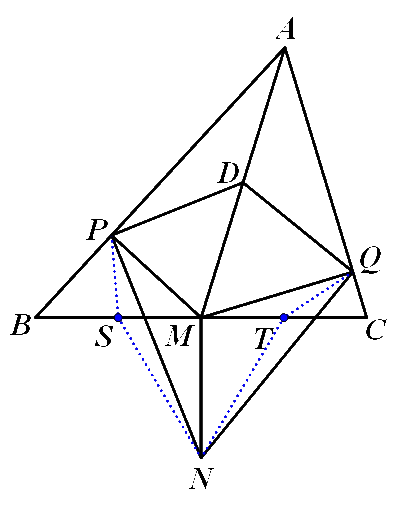
在Rt△BPM中,PS为斜边中线
∴PS=BM,同理可证QT=
BM
∵M为BC中点,∴BM=CM,∴PS=QT
∠NPS+∠BPS+∠APD=90°
∵∠BPS=∠B,∠APD=∠PAD
∴∠NPS+∠B+∠PAD=90°
又∠AMC=∠B+∠PAD
∴∠NPS+∠AMC=90°
∵∠NQT+∠DQT=90°
∠AMC=∠DMQ+∠QMT
∠DQT=∠DQM+∠MQT
又∵∠DMQ=∠DQM,∠QMT=∠MQT
∴∠AMC=∠DQT
又∴∠NPS=∠NQT
在△PSN和△QTN中
PN=QN,∠NPS=∠NQT,PS=QT
∴△PSN≌△QTN(SAS)
∴SN=TN,即△STN为等腰三角形
∵S是BM中点
∴SM=BM,同理TM=
CM
∵BM=CM
∴SM=TM
由等腰三角形的三线合一可得MN⊥ST,即MN⊥BC
知识点:直角三角形斜边上的中线
略
第二问构造直角三角形斜边的中线比较有难度,另外证明全等的倒角过程也比较复杂








