如图,以△ABC的AB、AC边为斜边向外作Rt△ABD和Rt△ACE,且使∠ABD=∠ACE=α,M是BC的中点.(1)求证:DM=ME;(2)求∠DME的度数.

答案
(1)分别取AB、AC的中点P、Q
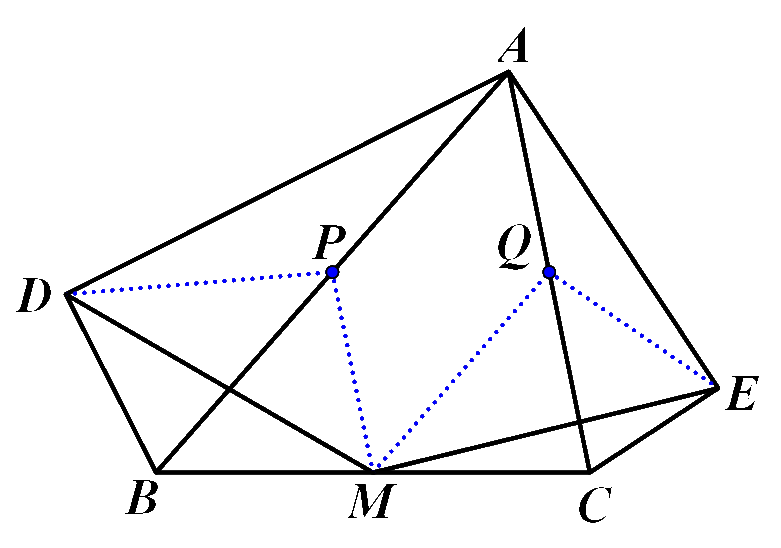
在Rt△ABD中,DP为斜边上的中线
∴DP=AB,同理QE=
AC
在△ABC中,P为AB中点,M为BC中点
∴PM∥AC且PM=AC,同理MQ∥AB且MQ=
AB
∴DP=MQ,PM=QE
在等腰△PBD中,∠PBD=α,∴∠DPB=180°-2α
同理∠CQE=180°-α
∴∠BPM=∠MQE
又∴∠DPM+∠BPM=∠CQE+∠MQC
即∠DPM=∠MQE
在△DPM和△MQE中
DP=MQ,∠DPM=∠MQE,PM=QE
∴△DPM≌MQE(SAS)
∴DM=ME
(2)∵△DPM≌△MQE
∴∠PDM=∠QME
∵MQ∥AB
∴∠BPM=∠PMQ
∴∠MDE=∠PMD+∠PMQ+∠QME
=∠PMD+∠BPM+∠PMD
=180°-∠DPB
=180°-(180°-2α)
=2α
知识点:直角三角形斜边上的中线 三角形中位线定理
略
如何将垂直关系和中点联系起来是这道题的关键








