（2011湖北）已知O₁与O₂相交于A、B两点，点O₁在O₂上，C为O₂上一点（不与A，B，O₁重合），直线CB与O₁交于另一点D．
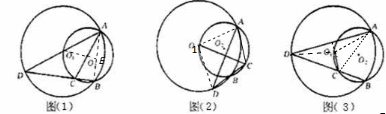
（1）如图（1），若AC是O₂的直径，求证：AC=CD；
（2）如图（2），若C是O₁外一点，求证：O₁C丄AD；
（3）如图（3），若C是O₁内的一点，判断（2）中的结论足否成立．

答案

（1）证明：连接AB，O₁O₂，
∵O₁与O₂相交于A、B两点，
∴O₁O₂⊥AB，
∵AC是圆O₂的直径，
∴∠ABC=90°，
∴O₁O₂∥BC，
∴∠D=∠AO₁O₂，
∵AC是直径，
∴∠AO₁C=90°，
∵O₂是AC的中点，
∴O₁O₂=O₂A，
∴∠AO₁O₂=∠0₁AC，
∴∠ADC=∠DAC，
∴AC=DC；
（2）证明：由（1）得：AC=DC，
∴C在AD的垂直平分线上，
∵O₁A=O₁D，
∴O₁在AD的垂直平分线上，
∴O₁C⊥AD；
（3）证明：∵AC=CD，
∴C在AD的垂直平分线上，
∵O₁A=O₁D，
∴O₁在AD的垂直平分线上，
∴O₁C⊥AD．

知识点：圆周角定理  圆与圆的位置关系  

（1）连接AB，O1O2，得到O1O2⊥AB，根据AC是圆O2的直径，推出∠ABC=90°，得出O1O2∥BC，根据三角形的中位线定理推出∠ADC=∠DAC即可得出AC=DC；
（2）根据线段的垂直平分线定理得到C在AD的垂直平分线上、O1在AD的垂直平分线上，即可得到答案；
（3）根据线段的垂直平分线定理得到C在AD的垂直平分线上、O1在AD的垂直平分线上，进一步推出结论．

主要考查了圆周角定理以及相交两圆的性质，根据相交两圆的连心线垂直平分两圆公共弦，以及垂直平分线的性质是解决问题的关键．

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>