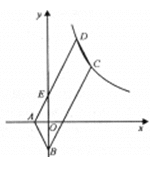
（2011湖北武汉市，16，3分）如图，平行四边形ABCD的顶点A，B的坐标分别是A（－1，0），B（0，－2），顶点C，D在双曲线y=上，边AD交y轴于点E，且四边形BCDE的面积是△ABE面积的5倍，则k=_____．

答案

如图，过C、D两点作x轴的垂线，垂足为F、G，DG交BC于M点，过C点作CH⊥DG，垂足为H，

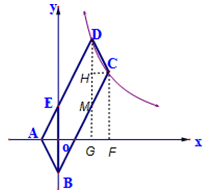
∵CD∥AB，CD=AB，
∴△CDH≌△ABO，
∴CH=AO=1，DH=OB=2，设C（m+1，n），D（m，n+2），
则（m+1）n=m（n+2）=k，
解得n=2m，
设直线AD解析式为y=ax+b，将A、D两点坐标代入得
-a+b=0m，a+b=2m+2，
解得 a=2，b=2，
∴y=2x+2，E（0，2），BE=4，
∴S_△ABE= ×BE×AO=2，
∵S_{四边形BCDE}=5S_△ABE，
∴S_△ABE+S_{四边形BEDM}=10，
即2+4×m=10，
解得m=2，
∴n=2m=4，
∴k=（m+1）n=3×4=12．
故答案为：12．

知识点：反比例函数综合题  

分别过C、D作x轴的垂线，垂足为F、G，过C点作CH⊥DG，垂足为H，根据CD∥AB，CD=AB可证△CDH≌△ABO，则CH=AO=1，DH=OB=2，由此设C（m+1，n），D（m，n+2），C、D两点在双曲线y=上，则（m+1）n=m（n+2），解得n=2m，设直线AD解析式为y=ax+b，将A、D两点坐标代入求解析式，确定E点坐标，求S_△ABE，根据S_{四边形BCDE}=5S_△ABE，列方程求m、n的值，根据k=（m+1）n求解．

不能熟练应用图形特征

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>