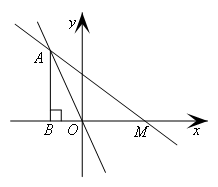
(11分)如图,已知一次函数y=kx+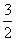 的图象经过点M(2,0),与正比例函数y=
的图象经过点M(2,0),与正比例函数y=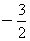 x的图象交于点A,过点A作AB垂直于x轴于点B.(1)求k值;并计算y=kx+
x的图象交于点A,过点A作AB垂直于x轴于点B.(1)求k值;并计算y=kx+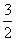 的图象与坐标轴围成的三角形的面积;(2)求交点A的坐标,计算AM的长;(3)在x轴上是否存在点P,使得以点P、A、M组成的三角形为等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
的图象与坐标轴围成的三角形的面积;(2)求交点A的坐标,计算AM的长;(3)在x轴上是否存在点P,使得以点P、A、M组成的三角形为等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.

答案
(1)解:将M(2,0)代入y=kx+![]() ,
,
得0=2k+![]() ,即k=
,即k=![]()
不妨记直线AM与y轴交于点C,则△MOC面积即为所求.
∵OC=![]() ,OM=2
,OM=2
∴![]() =
=![]()
(2)∵A为y=![]() x与y=
x与y=![]() 的交点
的交点
联立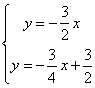
得,![]()
即A(-2,3)
∴AB=3,OB=2
在Rt△ABM中,AB=3,BM=4
由勾股定理得,AM=![]()
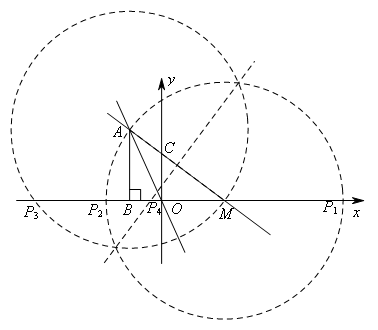
(3)
解:存在.![]() ,
,![]() ,
,![]() ,
,![]()
如图,以M为圆心,AM为半径作圆,交x轴于![]() 两点;
两点;
以A为圆心AM长为半径作圆交x轴于![]() ,作AM的垂直平分线交x轴于
,作AM的垂直平分线交x轴于![]() .
.
知识点:分类讨论——直角坐标系中线段转坐标、坐标转线段 一次函数表达式的确定 存在性问题
略
略








