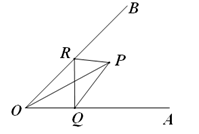
如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值是( )
- A.10
- B.
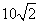
- C.
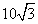
- D.12
答案
正确答案:B
知识点:轴对称的性质
如图,分别作点P关于OB、OA的对称点P1,,P2,由对称的性质,我们可得PR=P1R,PQ=P2Q,这样PR+RQ+PQ就转化成了P1R+RQ+P2Q,要求P1R+RQ+P2Q的最小值,只需让这三条线段在一条直线上,我们连接P1P2即可,接着我们连接OP1,OP2,由对称的性质可得OP=OP1=OP2=10,∠P1OB=∠BOP,∠P2OA=∠POA,又∠POB+∠POA=∠AOB=45°,所以∠P1OB+∠P2OA=45°,则∠P1OP2=90°,在Rt△P1OP2中,由勾股定理可得P1P2=![]()
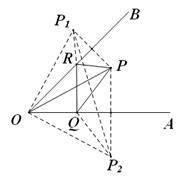
轴对称的性质,辅助线的做法








