(2011四川宜宾)如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转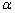 度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=
度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=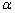 ,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中正确的是()
,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中正确的是()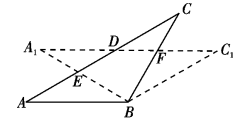
- A.①②⑤
- B.①②④
- C.①③④
- D.②③⑤
答案
正确答案:A
知识点:旋转的性质
解:①∠C=∠C1(旋转后所得三角形与原三角形完全相等)
又∠DFC=∠BFC1(对顶角相等)
∴∠CDF=∠C1BF=α
故结论①正确;
②∵AB=BC,
∴∠A=∠C,
∴∠A1=∠C,A1B=CB,∠A1BF=∠CBE,
∴△A1BF≌△CBE,
∴BF=BE,
∴A1B-BE=BC-BF,
∴A1E=CF;故②正确;
③在三角形DFC中,∠C与∠CDF=α度不一定相等,所以DF与FC不一定相等,故结论③不一定正确;
④由△A1DE≌△CDF可得,A1D=CD,而从图可知CD<CE,则A1D<CE故结论④不正确;
⑤BC=A1B,∠A1=∠C,∠A1BF=∠CBE
∴△A1BF≌△CBE
那么A1F=CE.故结论⑤正确.故答案为:①②⑤.
本题考查旋转的性质,其中涉及三角形全等的定理和性质:角角边、边边角证明三角形全等,全等三角形对应边相等,学生往往在这方面容易出错。








