在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.
(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求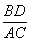 的值.
的值.

答案
解:(1)由题意知∠BOD=∠1=45°,此时△OBD是等腰直角三角形
∴OB=BD,OB⊥BD
∴AO=BD,AO⊥BD
(2)如图2,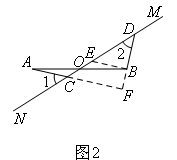
过点B作BE//AC交CD于点E,延长AC,DB交于点F.
∴∠DEB=∠DCF=∠1=45°,∠ACO=∠BEO,∠OAC=∠OBE
∴△BED,△FCD是等腰直角三角形
∴BD=BE,AC⊥BD
∵AO=BO
∴△AOC≌△BOE,
∴AC=BE
∴AC=BD,AC⊥BD
(3)如图3,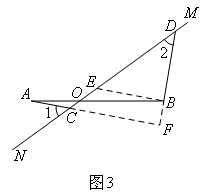
过点B作BE//AC交CD于点E,延长AC,DB交于点F.
∴∠DEB=∠DCF=∠1=45°,∠ACO=∠BEO,∠OAC=∠OBE
∴△BED、△FCD是等腰直角三角形,且△AOC∽△BOE
∴BD=BE,![]()
∵OB是OA的k倍
∴![]() =k
=k
∴![]()
知识点:相似中的类比探究问题
略
略








