在矩形ABCD中,E是BC的中点,点F在BC的延长线上,CM平分∠DCF,连接AE,作EM⊥AE交CM于点M.
(1)如图1,当AB=BC时,请判断AE与EM的数量关系并证明;
(2)如图2,当AB=nBC时,请判断AE与EM的数量关系并证明;
(3)如图3,把题目中“E是BC的中点”改为“BE=mEC”,当AB=nBC时,请判断AE与EM的数量关系并证明.

答案
解:(1)AE=EM,理由如下:
如图1,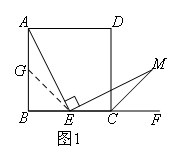
取AB的中点G,连接GE.
∵∠AEM=90°
∴∠MEC+∠AEB=90°
∵∠B=90°
∴∠EAG+∠AEB=90°
∴∠EAG=∠MEC
∵点E,G分别为正方形ABCD的边BC和AB的中点
∴AG=EC
∵△BGE是等腰直角三角形
∴∠AGE=135°
∵CM平分∠DCF
∴∠ECM=135°
∴△AEG≌△EMC
∴AE=EM
(2)当AB=nBC时,AE=(2n-1)EM,理由如下:
如图2,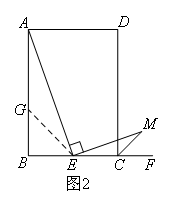
在AB上截取BG=BE,连接GE,则△BGE为等腰直角三角形
∴∠BGE=45°
∴∠AGE=∠ECM=135°
∵∠AEM=90°
∴∠MEC+∠AEB=90°
∵∠B=90°
∴∠EAG+∠AEB=90°
∴∠EAG=∠MEC
∴△AEG∽△EMC
∴![]()
∵AB=nBC,BC=2BE=2EC,BG=BE
∴AG+BG=2nEC
∴AG=(2n-1)EC
∴![]() =(2n-1)
=(2n-1)
∴AE=(2n-1)EM
(3)当AB=nBC,BE=mEC时,AE=(mn+n-m)EM,理由如下:
如图3,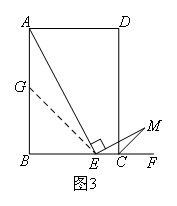
在AB上截取BG=BE,连接GE,则△BGE为等腰直角三角形
∴∠BGE=45°
∴∠AGE=∠ECM=135°
∵∠AEM=90°
∴∠MEC+∠AEB=90°
∵∠B=90°
∴∠EAG+∠AEB=90°
∴∠EAG=∠MEC
∴△AEG∽△EMC
∴![]()
∵BE=mEC
∴BC=BE+EC=(m+1)EC
∵AB=nBC,BG=BE
∴AG+BG=n(m+1)EC
∴AG+mEC=n(m+1)EC
∴AG=(mn+n-m)EC
∴![]() =(mn+n-m)
=(mn+n-m)
∴AE=(mn+n-m)EM
知识点:相似中的类比探究问题
略
略








