如图所示,在四边形ABCD中,AD∥BC,∠A的平分线AE交DC于E,AB=10,当BE是∠ABC的平分线时,AD+BC= ( ) 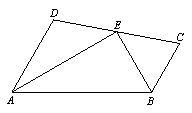
- A.5
- B.10
- C.8
- D.20
答案
正确答案:B
知识点:角平分线的性质
方法一:在线段AB上截取AF=AD,连接EF,易得△ADE≌△AFE(SAS),所以∠ADE=∠AFE,且有AD=AF. 已知AD∥BC,所以∠ADE+∠BCE=180°(两直线平行,内错角互补);看图可知,∠AFE+∠BFE=180°,所以易得∠BCE=∠BFE. 在△BEF和△BEC中,∠BFE=∠BCE,∠FBE=∠CBE,BE公用,所以△BEF≌△BEC,得BF=BC. AD=AF,BF=BC,所以AD+BC=AF+BF,即AD+BC=AB=10. 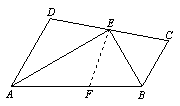 方法二:过点E做EF∥AD交AB与点F. ∵EF∥AD,∴∠DAE=∠AEF;已知AE是∠A的平分线,∴∠DAE=∠FAE. 在△AEF中,∠AEF=∠DAE,∠FAE=∠DAE,∴△AEF为等腰三角形,AF=EF.同理△BEF为等腰三角形,BF=EF. 从而点F为线段AB的中点,即AB=2EF. ∵F为线段AB的中点,EF∥AD∥BC,∴AD+BC=2EF. 从而可得AD+BC=AB=10.
方法二:过点E做EF∥AD交AB与点F. ∵EF∥AD,∴∠DAE=∠AEF;已知AE是∠A的平分线,∴∠DAE=∠FAE. 在△AEF中,∠AEF=∠DAE,∠FAE=∠DAE,∴△AEF为等腰三角形,AF=EF.同理△BEF为等腰三角形,BF=EF. 从而点F为线段AB的中点,即AB=2EF. ∵F为线段AB的中点,EF∥AD∥BC,∴AD+BC=2EF. 从而可得AD+BC=AB=10. 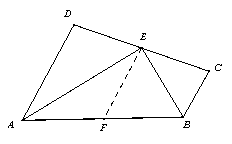
略








