（2011山东烟台）如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上．直线CB的表达式为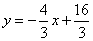
，点A、D的坐标分别为（－4，0），（0，4）．动点P自A点出发，在AB上匀速运动．动点Q自点B出发，在折线BCD上匀速运动，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）．（1）求出点B、C的坐标；（2）求S随t变化的函数关系式；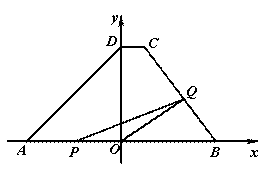
，点A、D的坐标分别为（－4，0），（0，4）．动点P自A点出发，在AB上匀速运动．动点Q自点B出发，在折线BCD上匀速运动，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）．（1）求出点B、C的坐标；（2）求S随t变化的函数关系式；
答案
（3）①在0＜t＜4时，当t＝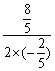
＝2时，S最大＝
＝
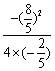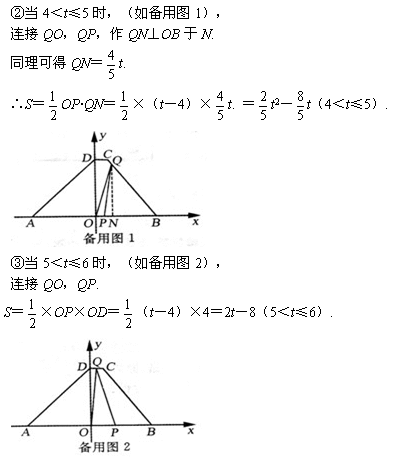
.②在4＜t≤5时，对于抛物线S＝
t2－t，当t＝－
＝2时，S最小＝×22－×2＝－.∴抛物线S＝t2－t的顶点为（2，－）.∴在4＜t≤5时，S随t的增大而增大.∴当t＝5时，S最大＝×52－×5＝2.③在5＜t≤6时，在S＝2t－8中，∵2＞0，∴S随t的增大而增大.∴当t＝6时，S最大＝2×6－8＝4.∴综合三种情况，当t＝6时，S取得最大值，最大值是4.
知识点：二次函数综合题
（1）把y=4代入y=- 43x+ 163，求得x的值，则可得点C的坐标，把y=0代入y=- 43x+ 163，求得x的值，即可得点B的坐标；（2）作CM⊥AB于M，则可求得CM与BM的值，求得∠ABC的正弦值，然后分别从0＜t＜4时，当4＜t≤5时与当5＜t≤6时去分析求解即可求得答案；（3）在（2）的情况下S的最大值，然后比较即可求得答案．
此题考查了点与函数的关系，三角形面积的求解方法以及利用二次函数的知识求函数的最大值的问题．此题综合性很强，难度较大，解题时要注意分类讨论思想，方程思想与数形结合思想的应用
WORD格式（
