如图,在Rt△ABC中,∠ACB为90°,CD⊥AB,cos∠BCD= ,BD=1,则边AB的长是( )
,BD=1,则边AB的长是( )

- A.
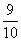
- B.
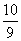
- C.
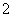
- D.
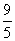
答案
正确答案:D
知识点:解直角三角形
解:在Rt△BCD中,cos∠BCD=![]() ,
,
设CD=2a,则BC=3a,
根据勾股定理得,12+(2a)2=(3a)2,
∴a=![]() ,∴BC=
,∴BC=![]() .
.
∵∠BCD=∠BAC,∴cos∠BCD=cos∠BAC.
设AC=2b,
则AB=3b,
在Rt△ABC中,由勾股定理得,(3b)2-(2b)2=![]() ,
,
解得b=![]() ,∴AB=
,∴AB=![]() ×3=
×3=![]() .故选D
.故选D
略








