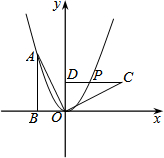
如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,顶点B在x轴负半轴上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
- A.
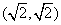
- B.
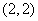
- C.
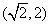
- D.
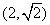
答案
正确答案:C
知识点:二次函数综合题
∵Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,
∴4=a×(-2)2,解得a=1
∴抛物线的解析式为y=x2.
∵Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴OD=OB=2,CD∥x轴,
∴点P的纵坐标为2,
∴令y=2,得2=x2,解得:x=±![]() ,
,
∵点P在第一象限,
∴点P的坐标为(![]() ,2).故选C.
,2).故选C.
略








