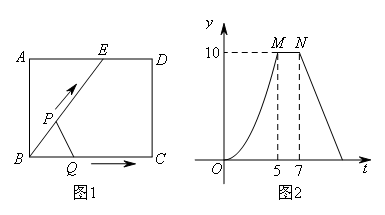
如图1所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿线段BC运动到点C时停止,且它们运动的速度都是1cm/s.设P,Q两点出发t s时,△BPQ的面积为ycm2.已知y与t的函数关系如图2所示(曲线OM为抛物线的一部分).则下列结论错误的是( )
- A.AD=BE=5cm
- B.cos∠ABE=
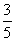
- C.当0<t≤5时,y=
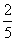 t2
t2 - D.当t=
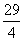 时,△ABE∽△QBP
时,△ABE∽△QBP
答案
正确答案:B
根据图2可得,当点P到达点E时点Q到达点C,
∵点P,Q运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5cm,故A选项中结论正确;
又∵从M到N时间的变化是2s,
∴ED=2 cm,
∴AE=AD-ED=5-2=3 cm,在Rt△ABE中,AB=![]() =4 cm,
=4 cm,
∴cos∠ABE=![]() ,故B选项中结论错误;
,故B选项中结论错误;
如图1,过点P作PF⊥BC于点F,
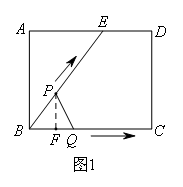
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=![]() ,
,
∴PF=PBsin∠PBF=![]() ,
,
∴当0
故C选项中结论正确;
当![]() 时,点P在CD上,
时,点P在CD上,
此时,PD=![]() -BE-ED=
-BE-ED=![]() -5-2=
-5-2=![]() cm,
cm,
PQ=CD-PD=4-![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵∠A=∠Q=90°,
∴△ABE∽△QBP,故D选项中结论正确.
故选B.
略








