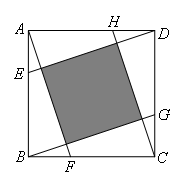
如图,E,F,G,H分别为正方形ABCD的边AB,BC,CD,DA上的点,且AE=BF=CG=DH=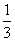 AB,则图中阴影部分的面积与正方形ABCD的面积之比为( )
AB,则图中阴影部分的面积与正方形ABCD的面积之比为( )
- A.
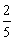
- B.

- C.
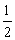
- D.
答案
正确答案:A
知识点:勾股定理 面积问题 全等三角形的判定与性质
解:如图,记CH与DE,BG分别相交于点M,N;记AF与DE,BG分别相交于点P,Q,
设正方形的边长为3a,DH=CG=a
∵BC=CD,∠BCG=∠CDH
∴△BCG≌△CDH
∴∠CBG=∠DCH
∴∠CBG+∠NCB=∠DCH+∠NCB=90°
∴∠BNC=90°
同理可得,∠CMD=90°
∴△BCN≌△CDM
同理可证:△BCN≌△CDM≌△DAP≌△ABQ
即:此图形为赵爽弦图,阴影部分为正方形,
在Rt△CDH中,由勾股定理得![]() ,
,
由面积公式得![]() ,
,
∴![]() ,
,
在Rt△DMH中由勾股定理得![]() ,
,
则![]() ,
,
∴阴影部分的面积:正方形ABCD的面积=![]() .
.
故选A.
略








