如图，已知：正方形ABCD中，∠BAC的平分线交BC于E，下列选项中正确的是（ ）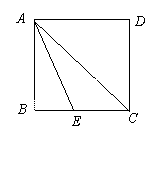
- A.AB+BE=AC
- B.AE+EC=AC
- C.AB+EC=AC
- D.AE+BE=AC
答案
正确答案：A
知识点：旋转对称图形
证明：延长EB到点F，使BE=BF，四边形ABCD是正方形，所以AB=BC 则AB+BE=BC+BF=CF。在Rt△ABF和Rt△ABE中 AB=AB，BF=BE，∴Rt△ABF≌Rt△ABE（HL），∴ ∠2=∠3。又AE是 ∠BAC的角平分线，所以 ∠2=∠1=22.5° 。又∠F+∠3=90° 。所以∠F=67.5° 而∠FAC=∠1+∠2+∠3=3∠1=67.5° ，∴ ∠FAC=∠F，所以AC=CF即得证AB+BE=AC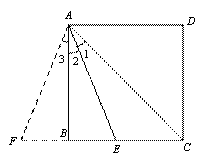
略
WORD格式（
