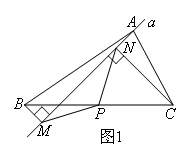
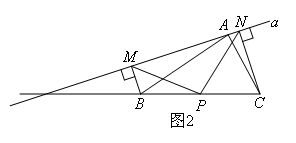
如图1,在△ABC中,P为BC边的中点,直线a绕顶点A旋转,若B,P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM,PN.要证PM=PN,只需延长MP交CN于点E,通过说明某对三角形全等,进而用直角三角形斜边中线等于斜边一半就可以得到.若直线a绕点A旋转到图2的位置时,点B,P在直线a的同侧,其他条件不变,要证明PM=PN,我们可以进行和上面一样的操作,则需要证明的全等三角形是( )
- A.△APB≌△APE
- B.△CAN≌△ABM
- C.△NPB≌△NPE
- D.△MBP≌△ECP
答案
正确答案:D
知识点:倍长中线法 中考数学几何中的类比探究
按照要求,作出符合题意的辅助线:延长MP交CN于点E.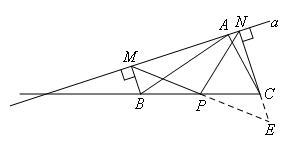
则△MBP≌△ECP,
∴PM=PE,
则在Rt△NME中,PM=PN,
∴要证明PM=PN需要证明△MBP≌△ECP.
略









