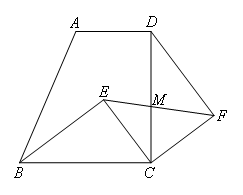
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD.E为梯形内一点,且∠BEC=90°,
将△BEC绕C点旋转90°使BC与DC重合,得到△DFC,连EF交CD于M.已知BC=5,CF=3,则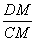 的值为( )
的值为( )
- A.5:3
- B.3:5
- C.4:3
- D.3:4
答案
正确答案:C
知识点:勾股定理 旋转的性质 相似三角形的判定与性质
由旋转性质得,CE=CF=3,CB=CD=5,
∠BEC=∠DFC=90°,∠BCE=∠DCF.
∵∠BCD=∠BCE+∠ECD=90°,
∴∠ECF=∠DCF+∠ECD=90°,
∴∠ECF+∠DFC=180°,
∴EC∥DF,
∴△ECM∽△FDM,
∴![]() .
.
在Rt△DCF中,由勾股定理得,DF=4.
∴![]() .
.
略








