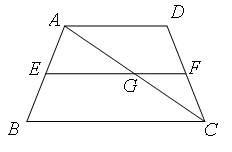
如图，等腰梯形ABCD中，AD∥BC，中位线EF交AC于G，且AC平分∠BCD，EG=a，GF=b，.则梯形ABCD的周长为（ ）.

解：由EF为梯形中位线得：E，F为中点，且EF∥BC，EF∥AD
从而G为AC的中点
∴EG为△ABC的中位线，FG为△ACD的中位线
∴BC=2a，AD=2b
∵AD∥BC
∴∠DAC=∠ACB
∵AC平分∠BCD
∴∠ACD=∠ACB
∴∠DAC=∠ACD
从而AD=DC=2b
∵梯形ABCD为等腰梯形
∴AB=DC=2b
∴梯形ABCD的周长=2a+6b

得不出AD=CD