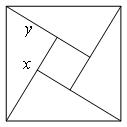
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x²+y²=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是(    )

1．思路分析：
①识别弦图模型．本题中四个全等的直角三角形组成的正方形是弦图的主要特征．
②整合条件，验证结果．根据弦图特征及大小正方形面积表达直角三角形边长的间关系，进而验证四个选项的正误情况．
2．解题过程：
如图，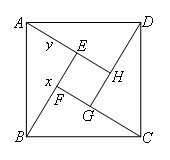

在Rt△ABE中
由勾股定理得，
∵
∴，①正确．
∵△AEB≌△BFC
∴AE=BF
∴x-y=EF
∵EF²=4
∴x-y=2，②正确．
∵
∴49=4+2xy，③正确．
∵，49=4+2xy
∴，④不正确
∴①②③正确，选B．
3．易错点
未能将大正方形的面积与勾股定理联系起来，难以判断①②
对弦图模型及其证明不熟悉，不能转化为③来求得正确结果．

略